Marc Pradas
Senior Lecturer in Applied Mathematics
My research interests cover a wide range of topics on the interface of applied mathematics, statistical physics, and engineering science. I give particular emphasis on soft condensed matter theory and fluid dynamics, including multiphase flows, microfluidics, and hydrodynamic instabilities. I'm also interested in stochastic/chaotic processes and emergent collective phenomena in complex and biological dynamical systems.
Part of my research is funded by EPSRC. I was a co-investigator of the project EP/L027186/1--Fluid processes in smart microengineered devices: Hydrodynamics and thermodynamics in microspace during 2015-2019, and I was the principal investigator of the project EP/R041954/1--Droplets with dynamic size on smooth surfaces, in which we explored the interplay between a time-dependent variation of the volume of a sessile droplet (as a consequence of, e.g., evaporation/condensation) and simple smooth variations on solid surfaces.
Research Highlights
Evaporating droplets on smooth patterns
Droplets evaporating on a solid surface are normally affected by contact line pinning, which is caused by microscopic surface roughness. We have recently shown that smooth, pinning-free, solid surfaces with either non-planar topography or chemical patterns promote a reproducible sequence of well-defined droplet configurations paced by dynamic snap events, which are triggered by a hierarchy of bifurcations.
Wells et al., Nature Communications, 2018
Ewetola et al., Physics of Fluids, 2021

Capillary microseparators
Capillary microseparators are used in many technological applications involving two-phase flow at the microscale. A typical device consists of a series of small capillaries regularly spaced which are interconnected to a microchannel for which a gas-liquid (multiphase) flow is passing through. Our work has focused on understanding the dynamics of the gas-liquid flow through the capillaries to quantify the operability region of the device.


Falling liquid films
A liquid film falling down an inclined plane is an example of a convectively unstable open-flow hydrodynamic system that is characterised by a very rich dynamics in terms of wave evolution and transitions. At the latest stage of the evolution, the film surface is dominated by interacting solitary waves, which under certain conditions may form bound states, i.e. groups of waves travelling with the same speed. We have done extensive work to characterise weak interactions between pulses, and we are currently working towards understanding the emergence of oscillatory states as a consequence of strong interactions.
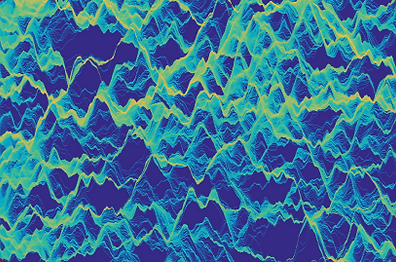
Convergent chaos & lacunarity exponents
Chaos is widely understood as being a consequence of sensitive dependence upon initial conditions, which generally means that chaotic trajectories separate exponentially. However, we have shown that despite the overall intrinsic instability of chaotic systems, trajectories may be very strongly convergent in phase space over very long periods. This convergent phenomenon can lead to intense particle clustering with density distributions described by well-defined power laws.
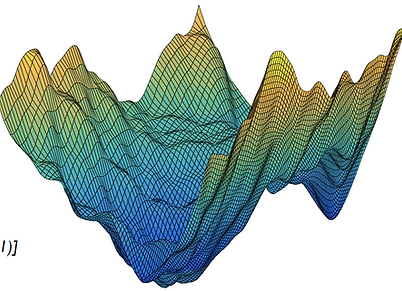
Noise-induced transitions in multiscale systems
External or internal random fluctuations are ubiquitous in many physical and technological systems and can play a key role in their dynamics. Many of these phenomena can be modelled by noisy dynamical systems characterized by the presence of a wide range of different time- and length-scales interacting nontrivially with each other. Our work has focused on understanding the main effects of additive noise on multiscale systems, observing the emergence of noise-induced critical transitions and intermittency. We are also interested in quantifying the interplay between noise and small scale spatial fluctuations and how this can lead to deviations from the macroscopic averaged behaviour.